DEEP IMPACT

　　　


impact時に放出されたダストによるダストテイルの予想
上の映像は、Celestiaに、Jestr Jack氏によるデータを組み込んで作成したもの。
Written by K. Sugawara Jun.16, 2005　Updated on Jun.16, 2005

概要


　2005年7月４日のDeepImpactによるTempel第１周期 彗星(9P/Tempel)の核へのimpactorの衝突により 飛び散ったダストが、
地上からダストテイルとして観測された場合、どのような形状になり、どのような時間変化をするかシミュレーションを行った。


計算条件

  1. 　仮定
    • impactの瞬間に、ダストはimpactorの進 行方向と逆方向に軸を持つcone上の様々な方角に、瞬間的に同時に放出される。
    • 放出時刻＝impactの時刻は、2005年7月4日6時UTとする。
    • impactorの軌道は、JPL's HORIZONS Systemに よる値を用いた。
    • その後、ダストは太陽からの光圧と重力に支配されて運動を続ける。
    • 彗星核との重力、ガスの抵抗等の力は無視できるものと仮定。太陽とダストの２体問題とし、運動方 程式を解く。
    • 彗星核本体の運動は、　Orbital Elements: MPC formatの軌道要素を用いて計算。
  2. 　以下のパラメータの組み合わせを様々に設定し、7 月4.5日から40日後までの地球から見た形状の変化を数値積分 （Runge -Kutta法）で計算。GIFアニメーションにした。
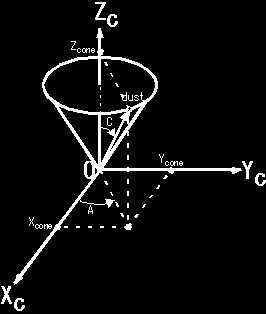
    • coneの頂角の半分の角度　C（下図参照）
    • ダストに働く重力に対する光圧の比　β　（概ねβが大きいほど小さなダストと考えてよい）
    • ダストの彗星核に対する相対的なspeed　V
  3. 　βについては、過去の彗星のダストテイルで観測された値を参考とした。
  4. 　C、Vについては、予想が非常に難しいため、適当に設定した値である。逆に、観測結果から、これら の値を決定できる可能性がある。
  5.  　図の原点（中央）が彗星核の位置。右が西、上が北の方向。
  6. 　１本の円は、 同じβ（ダストに働く重力に対する光圧の比）を持つダストの集合。こ の計算では、βを、０から2.0まで20段階にわけて計算している。一番左側がβ=2.0、右側がβ＝0.0．実 際には、βは離散的にではなく、連続的に分布しているので、図のよ うな円の集合として｢しましま模様｣に見えるわけではない。あえて言えば、チューブ状に見え ると言ったほうが実際に近いだろう。
  7. 　各円の中心を 結んだ曲線が、いわゆるシンクロン曲線に相当する。通常の Bessel-Bredkin法では、ダストの相対速度は０と仮定する。こ の計算では、初速を与えているので、その分シンクロン曲線が太くなっていると考えればよい。 時間とともに、円の直径は大きくなっていく。
  8. 　この計算では、ダストの量（空間密度。 今回の場合、impact時に放出されるダストの量と言い換えてもよい）は一切考慮していない。力学的にそこにダストが分布する可能性を示しているだけ で、実際に観測されるかどうかは、ダストの量に大きく依存する。また、impactと無関係に形成されたコマやテイルと重なって見えるので、さらに複雑な 姿になるだろう。この計算は、あくまで、様々なパラメータの値を仮定 した上で描いたもので、｢このように見える｣と主張しているわけではない。なぜなら、パラメータの値は、ほとんど予測不能なものであるから だ。パラメータを変えると出力される図も変化する。
  9. 　観測データを得た後で、その結果にあう ように、パラメータを様々に変化させることで、パラメータを決定、すなわちimpact時に何が起きたのかを知ることができる。今回の計算は、そのための 予備計算であ ることをご理解いただきたい。
  10. このサンプル計算による尾の発達の様子 は、次のように解釈することができる。

シミュレーション結果

図によってスケール（描画領域の範囲）が異なることに注意

●ダストの初速度　V　＝　１．０[km/s]

●ダストの初速度　V　＝　０．０１[km/s]


●通常のシンクロン曲線　ダストの初速度　V　＝　０　の場合



●詳細は、以下で発表の予定。
    Dust Tail of Comet 9P/Tempel 1 after the Deep Impact: Prediction (Abstract: Planetary Scienceより)
    AOGS 2005, the Asia Oceania Geosciences Society's 2nd Annual Meeting
●関連情報


DeepImpactのページへ戻る